< 목차 >
- 용어정의
- Bias vs. Variance
1. 용어정의
- Bias : 실제값에 대한 추정값의 오차
- Variance : 측정값의 퍼짐정도

2. Bias vs. Variance
앞에서 언급한 overfitting을 방지하기 위해 Error functions에 regularization term을 도입하였고, 이때 lambda 라는 적절한 regularization coefficient 의 설정이 필요하다.
따라서 본 내용에서는 최적의 λ 를 어떻게 찾는지에 대해 Bias 와 Variance를 이용하여 설명한다.
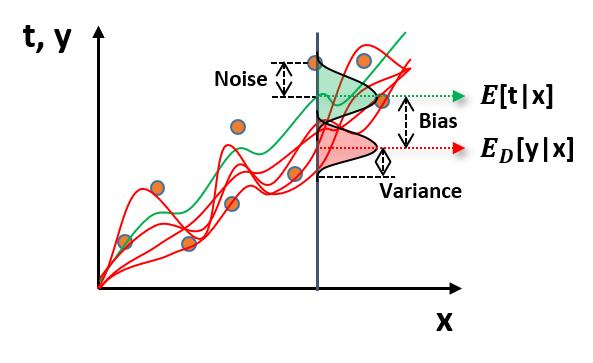
y-t 를 최소화하는 예측모델링을 할 때, 다음 Noise, Variance, Bias 의 세 가지 요소가 존재한다.
(1) Noise
- 수집데이터(주황색 점)들은 기대값(연두색 선) E[t|x] 를 기준으로 랜덤성분을 갖는다. 이러한 랜덤성분은 Noise라고 한다.
(2) Variance
- 데이터를 수집하고 매 차례 반복적으로 모델링(빨간색 선)을 한다면, 예측 모델에 대한 정밀도를 알 수 있고, 이를 분산(Variance)라고 한다.
(3) Bias
- 타겟데이터들의 기대값 E[t|x] 과 수많은 예측모델들의 기대값 ED[y|x] 에 대한 오차를 Bias 라고 한다.
Noise는 데이터 내재적 요인으로 발생하는 랜덤성분이기 때문에 통제가 불가하고, Variance와 Bias 의 경우에는 조절가능하다. 즉, 'y-t = Noise + Bais + Variance' 로 나타낼 수 있다. 아래의 Loss function을 최소화하는 방법으로 최적의 λ 를 찾을 수 있는데, 여기서 y(x)에 대해 양변을 편미분하면 아래의 수식으로 전개될 수 있다.
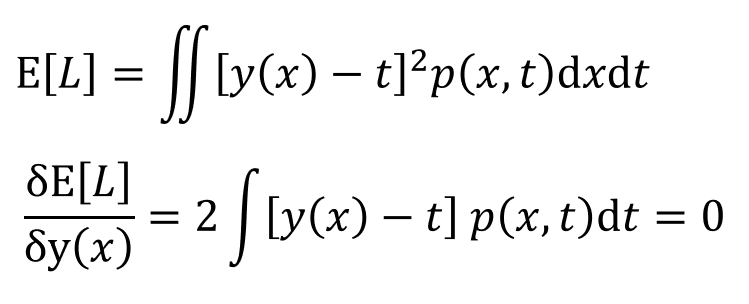
여기서 y(x)에 대해 풀어보면 y(x)가 타겟데이터들의 기대값인 E[t|x] 일 경우에 Loss function인 E[L]이 최소화되는 것을 알 수 있다. (여기서는 수식전개 편의를 위해 h(x)라고 두었음)
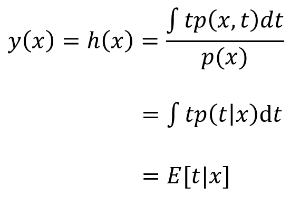
이러한 h(x)를 이용하여 앞서 언급한 Loss function에서 (y(x)-t)^2 의 항을 다시 해석할 수 있고, y(x)와 타겟데이터의 Noise에 관한 항을 얻을 수 있다. 여기서 '-h(x) + h(x)' 항을 가운데 추가하여 전개하였고, 맨 뒷부분은 h(x)가 t에 대한 기대값을 뜻하기 때문에 전체 타겟데이터 t에 대해 적분할 경우, h(x)-t는 0이 되어 사라진다.
그러면 첫번째 항과 두번째 항만 남게되는데, 첫번째 항은 y(x)가 t에 대한 기대값에 가까워지면 Loss function이 최소가 된다는 항으로 y(x)에 모델링에 대한 내용이고, 두번째항은 t에 대한 기대값인 h(x)와 수집된 타겟데이터 간의 분산을 나타내는 것으로, 결국 'Noise'를 뜻한다.

이어서, 주어진 데이터셋에서 독립적인 확률분포 p(t,x)를 갖도록 추출된 부분데이터들로 y(w,x)를 수차례 모델링하였을 때, 이를 g(x) = ED[y(x;D)] 라고 둘 수 있다.
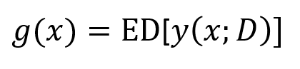
전체데이터셋에 대한 g(x) 들의 평균기대값을 E[y(x;D)]라고 두었을 경우, Loss function인 E[L]은 아래와 같이 나타날 수 있다. 그리고 D에 관한 기대값을 계산할 경우, 좌측의 수식으로 전개되며 맨 뒷부분의 항은 마찬가지로 y(x;D)와 g(x)의 기대값이 동일하기 때문에 사라진다. 역시나 첫번째항과 두번째항만 남게되는데 여기서 첫번째 항은 y(w,x)들에 대한 Variance 를 뜻하고, Bias 는 타겟데이터들의 기대값과 y(w,x)에 대한 기대값의 오차를 뜻한다.
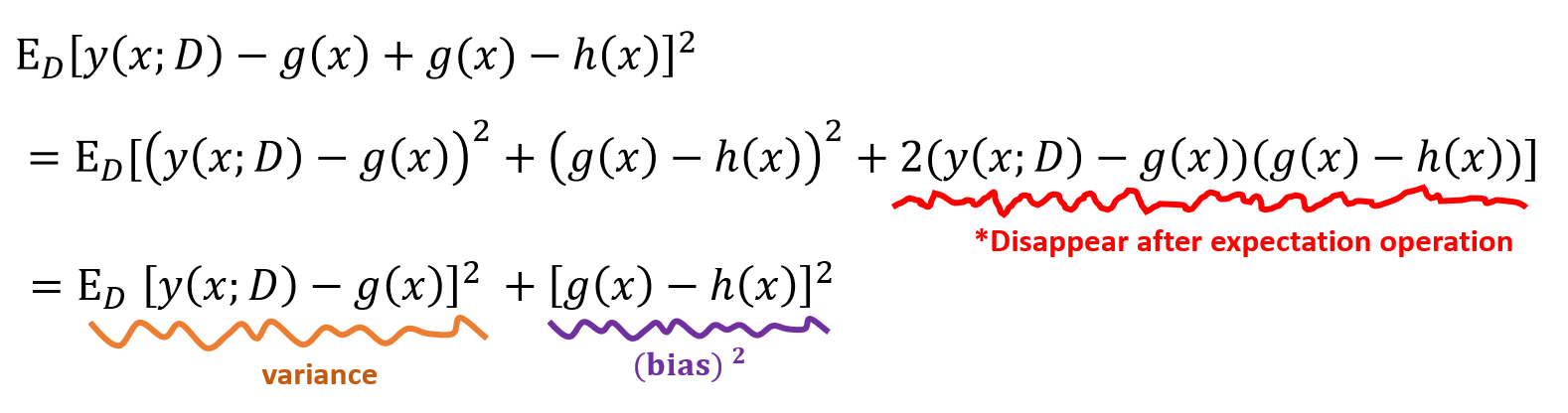
결국엔 Loss function인 E[L]은 다음과 같이 Bias와 Variance, Noise 에 대한 수식으로 표현할 수 있다.

아래는 위에서 전개한대로 여러차례 모델링하여 λ 의 변화에 따른 예측그래프 y(w,x)의 Variance 와 Bias 의 변화를 나타낸 것이다.
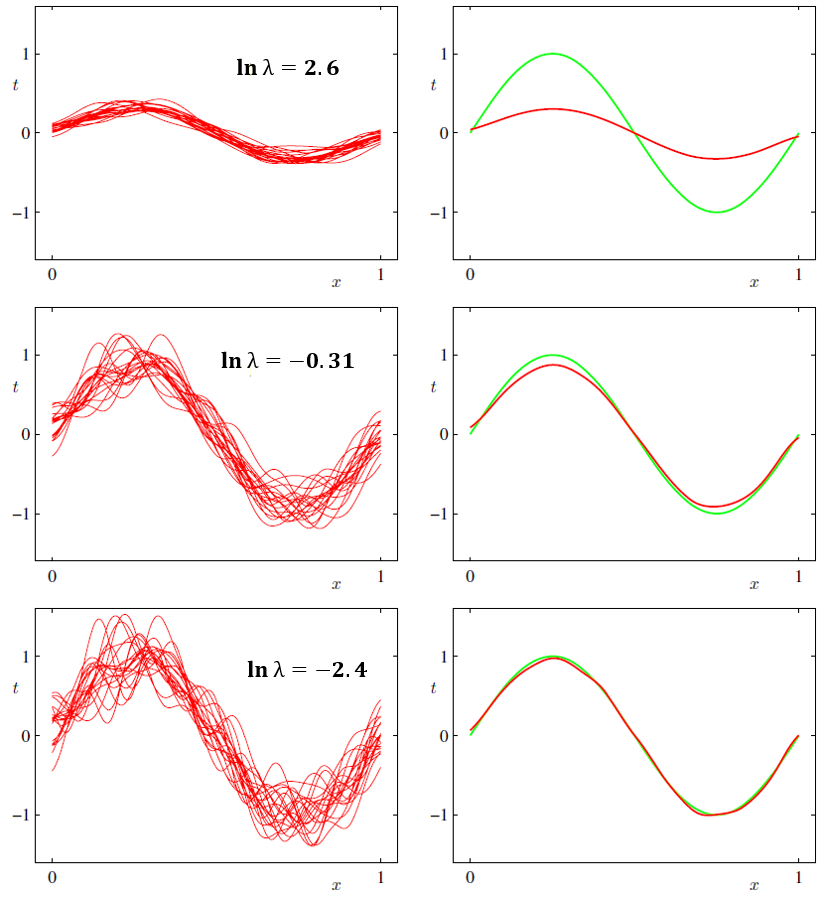
맨왼쪽 첫번째 줄의 그래프들은 예측모델들(다수의 빨간색 선)의 Variance를 나타낸 것이고, 두번째 줄의 그래프는 타겟데이터의 기대값(연두색 선)과 예측그래프(빨간색 석)의 기대값 오차인 Bias를 나타낸 것이다. 또한, Lambda가 증가하면, Variance가 증가하고 Bias는 감소한다. 반대로, λ 가 감소하면, Variance가 감소하고 Bias가 증가한다. 종합해보면 Variance와 Bias 사이에서 적절한 밸런스를 갖는 λ 를 선택하는 것이 필요하다.
결론적으로, 통제불가한 Noise를 제외하고 Bias와 Variance 사이에서는 Trade-off가 존재하며 test error를 최소화하는 것이 (Bias)^2 와 Variance 합이 최소가 되는 지점이라는 것을 알 수 있다. 즉, test error를 최소화하는 최적의 λ는 (Bias)^2 와 Variance 합이 최소가 되는 지점에서 선택된다.

'인공지능 > 머신러닝 이론' 카테고리의 다른 글
| 2-6. Overfitting and Condition Number (0) | 2021.03.29 |
|---|---|
| 2-5. Singular Value Decomposition(SVD) (0) | 2021.03.29 |
| 2-3. Regularized Least Squares (0) | 2021.03.29 |
| 2-2. Maximum Likelihood and Least Squares (0) | 2021.03.29 |
| 2-1. Linear Models for Regression (0) | 2021.03.29 |



