< 목차 >
- 용어정의
- Probabilistic generative models
1. 용어정의
아래 페이지를 참고해주세요.
2. Probabilistic generative models
앞장에서 언급했던 Generative model은 Class-conditional density function인 p(x|Ck) 와 Class prior probability인 p(Ck) 를 계산하고, 베이지안 이론을 통해 Posterior probability 인 p(Ck|x)를 계산한다. 이는 두 클래스를 갖는 Classification Problems에서 Sigmoid Function로 표현될 수 있다.

또한, K개의 클래스 문제에서는 다음과 같은 수식으로 전개될 수 있으며, 이를 Softmax function이라고 한다.

Probabilistic Generative Models을 살펴보기 위해서, Class-conditional density function이 정규분포를 갖고 모든 클래스가 동일한 공분산 매트릭스(Covariance)를 가진다고 가정하면 p(Ck|x)는 W에 관한 Linear model로 나타낼 수 있다.


W와 w0으로 표현된 Linear model은 위의 수식항을 가지는데 이를 하나씩 자세히 전개해보면, 동일한 공분산을 가지는 2차항의 x(Quadratic terms in x)는 지워지고 아래와 같이 Linear model로 표현된다.
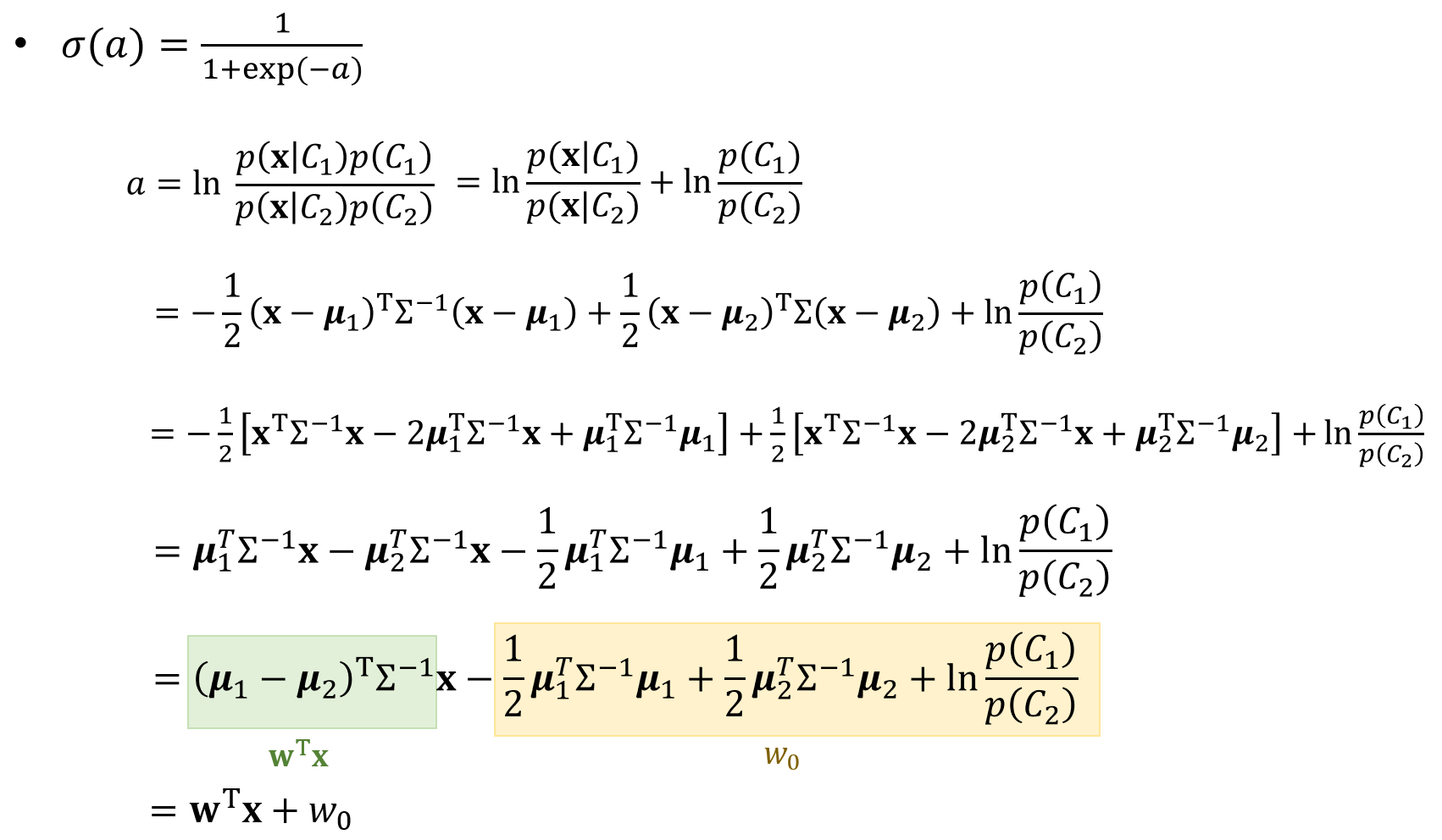
마찬가지로, K개의 클래스로 확장해나가면 다음과 같이 전개할 수 있고 동일하게 W에 관한 Linear model로 나타난다. 이때, 맨마지막 항(연두색 영역)은 모든 클래스에서 동일한 공분산 매트릭스를 가지므로 항상 일정한 Constant로 나타나 큰 역할을 차지하지 않아 무시할 수 있다.

위의 복잡한 수식에서 표현하는 의미는 아래의 그림으로 표현될 수 있다.

왼쪽의 첫번째 그림은 정규분포를 갖는 세 클래스의 class-conditional densities를 타나낸 것으로, 연두색과 빨간색 영역의 데이터는 동일한 공분산 매트릭스를 갖고 파란색 영역과는 다른 공분산 매트릭스를 갖는다.
이때 계산된 각각의 Posterior probability는 왼쪽 두번째 그림으로 나타날 수 있고, 동일한 공분산을 갖는 영역은 선형의 Decision boundary로 영역이 나눠지고, 다른 공분산을 갖는 영역에서는 비선형의 Decision boundary로 나눠지는 것을 확인할 수 있다.
즉, 입력데이터가 만약 동일한 형태의 분포를 가지고 있을 경우에 Linear Decision boundary 로 나타나고, 아닌 경우에는 Quadratic form의 비선형으로 나타난다. 하지만, 동일한 공분산을 갖지 않을 경우에도 비선형과 선형 Decision boundary는 분류에 큰 영향을 미치지 않으므로 앞의 수식에서 연두색 영역을 무시하고 선형적으로 근사할 수 있다.
'인공지능 > 머신러닝 이론' 카테고리의 다른 글
| 3-7. Linear Basis Function Model (0) | 2021.04.01 |
|---|---|
| 3-6. Estimation of the Class-Conditional & Prior Probabilities (0) | 2021.04.01 |
| 3-4. Fisher's Linear Discriminant (1) | 2021.03.31 |
| 3-3. Least Squares for Computing 'w' (0) | 2021.03.31 |
| 3-2. Discriminant Functions (0) | 2021.03.31 |



