< 목차 >
- 용어정의
- Margin of support vector machine(SVM)
- Classification of the perpendicular distnace to the decision surface
- Classification of margin
- Simplification of margin
1. 용어정의
- 피드백 후 작성예정입니다.
2. Margin
2-1. Calculation of the perpendicular distance to the decision surface
SVM에서 Margin의 개념은 굉장히 중요하기 때문에 수식전개를 통해 깊이있게 이해할 필요가 있다.
임의의 'x_A'와 'x_B'라는 데이터가 Decision boundary인 y(x) 위에 있다고 가정할 경우, 아래의 조건을 만족하고 이는 곧 'w' 벡터가 임의의 x성분간의 벡터에 수직이라는 것을 알 수 있다.

입력데이터 x가 Decision boundary에 있는 경우, y(x)=0 이므로 w에 관하여 b를 이항하고 양변에 ||w||에 관해 나누어서, 원점에서 Decision boundary까지의 Nominal distance를 다음과 같이 나타낼 수 있다.

반대로 입력데이터 x가 Decision boundary에 없는 경우, Decision boundary에 수직으로 사영시킨 'x⊥' 까지의 벡터와 Decision boundary에서 x까지의 벡터 'r' 의 합으로 벡터를 표현할 수 있는데, 여기서 r 벡터의 방향은 'w'와 동일하므로 w의 nominal vector에서 'r' 만큼 Scaling 해준다.

위의 x에 관한 벡터 양변에 'w'를 곱해주어, (1)과 같은 수식으로 전개할 수 있고, Decision boundary에 존재하는 'x⊥'와 존재하지 않는 'x'에 대해 다음의 y(x)에 관한 수식인 (2)로 나타낼 수 있다.

여기서 (2)의 각 항을 (1)에 대입하면, 아래와 같은 수식으로 전개할 수 있고, 동일 항을 제거하면 Decision boundary로 부터 'x'까지의 거리인 'r'에 대한 표현을 구할 수 있다.
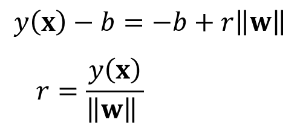
2-2. Calculation of Margin
위에서 구한 'r'은 수식을 보면 알 수 있듯 양수 혹은 음수일 수도 있으며, 이는 각 데이터에 대한 타겟데이터 곱해서 절대값의 수치로 표현할 수 있다.
이것이 가능한 이유는 입력데이터에 대한 y(x)가 음수일 경우에 타겟데이터는 -1에 해당할 것이며, y(x)가 양수일 경우에 타겟데이터는 +1에 해당하기 때문에 두 개의 곱은 항상 1이 되고, 절대거리로 나타낼 수 있다.
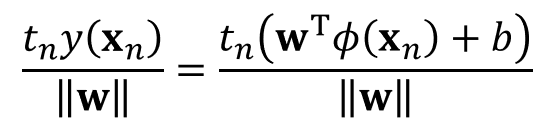
이때 'Margin'은 Decision boundary로부터 각 데이터간의 거리가 가장 가까운 것을 의미하며, 해당 위치에 존재하는 데이터가 Support vector 가 되는 것이다.

이렇게 Decision boundary로부터 최소한의 거리를 갖는 Support vector를 정하면, 각 클래스에 해당하는 Support vector 간의 거리를 최대화하기 위해 'w'와 'b'를 다시 업데이트한다.

2-3. Simplification of Margin
위의 수식은 Constraint를 통해서 풀기쉬운 간단하게 수식으로 표현될 수 있는데, 그때 Constraint에 대한 전제는 다음과 같다.

입력데이터 x가 support vector일 경우, y(x)의 양변에 |y(x)|를 취하면 -1 혹은 +1이 되며 이와 동일한 값을 갖는 오른쪽 항에 타겟데이터 값을 곱하면 무조건 1의 값을 갖는다. 위의 방식으로 생각하면, Support vector 가 아닌 모든 입력데이터에 대해서는 y(x) 값이 -1 이하이거나, 혹은 +1 이상이기 때문에 아래의 조건을 만족한다.

또한, y(x)의 값이 -1 혹은 +1의 값을 갖기 때문에 Decision boundary로부터 각 데이터까지의 거리는 다음의 Scaling에 영향을 받지않고, 이후 Support vector들은 1/||w|| 값에 점점 가까워 진다.

따라서 Margin은 다음의 Constraint 하에서 1/||w||을 최대화하는 문제로 간단하게 표현할 수 있으며 이는 곧 ||w||^2 을 최소화하는 것과 동일하며, 이것를 'Primary problem' 이라고 정의한다.

'인공지능 > 머신러닝 이론' 카테고리의 다른 글
| 6-4. Classification of a new data point (0) | 2021.04.05 |
|---|---|
| 6-3. Quadratic Optimization Problem (0) | 2021.04.05 |
| 6-1. Overview of Support Vector Machine(SVM) (0) | 2021.04.05 |
| 5-5. Introduction to Support Vector Machines(SVM) (0) | 2021.04.04 |
| 5-4. Radial Basis Function(RBF) Neural Network (0) | 2021.04.04 |



