< 목차 >
- 용어정의
- 행렬 분해의 이해
- 확률적 경사하강법(SGD)를 이용한 행렬 분해
- 확률적 경사하강법(SGD) 활용예제
- 행렬 분해를 이용한 개인화 영화 추천시스템 개발
1. 용어정의
- 피드백 후 작성예정입니다.
- MovieLens 데이터셋은 데이터셋 자료실 에 있습니다
2. 행렬 분해의 이해
행렬 분해는 다차원 매트릭스를 저차원 매트릭스로 분해하는 기법으로 대표적으로 SVD(Singular Value Decomposition), NMF(Non-Negative Matrix Factorization) 등이 있습니다.
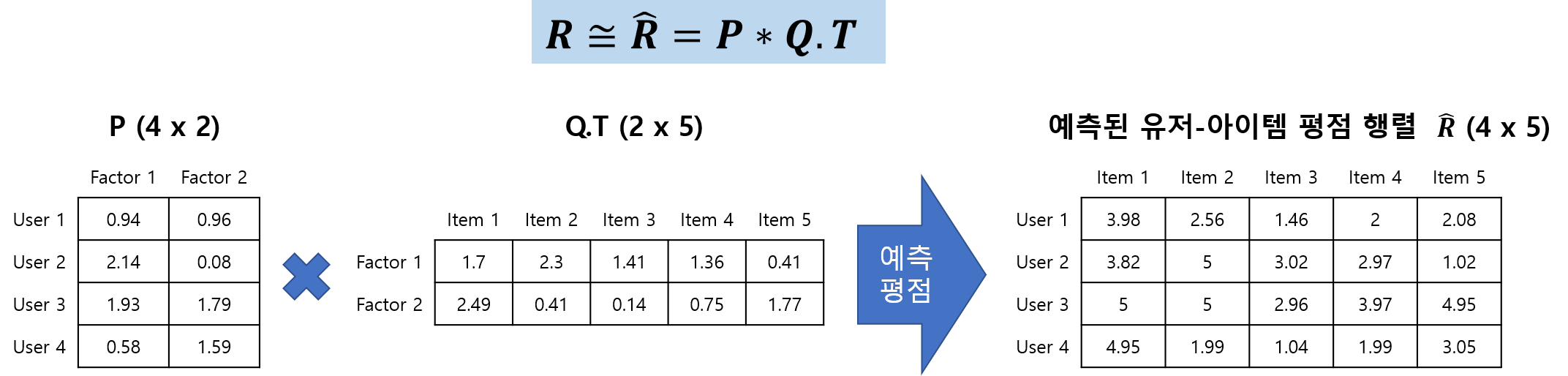
즉, M개의 사용자(User) 행과 N개의 아이템(Item) 열을 가진 평점 행렬 R은 M X N 차원으로 구성되며, 행렬 분해를 통해 사용자-K 차원의 잠재 요인 행렬 P (M X K 차원)와 K 차원의 잠재 요인ㅡ아이템 행렬 Q.T (K X N 차원)으로 분해될 수 있다. 따라서, R = P * Q.T 이며, 아래 그림과 같이 나타낼 수 있다.

예로 들면, R 행렬의 u행 사용자와 i열 아이템 위치에 있는 평점 데이터를 r(u,i)라고 하면, P행렬과 Q.T 행렬의 곱을 통해 평점데이터를 유추할 수 있다.


위의 계산에서 보듯, 사용자ㅡ아이템 평점 행렬의 미정 값을 포함한 모든 평점 값은 행렬 분해를 통해 얻어진 P와 Q.T행렬의 내적을 통해서 예측 평점으로 다시 계산할 수 있다.
3. 확률적 경사하강법(SGD)를 이용한 행렬 분해
R 행렬을 P와 Q 행렬로 분해하기 위해서는 주로 SVD 방식을 이용하나, 이는 널(NaN) 값이 없는 행렬에만 적용할 수 있다. R 행렬은 대부분의 경우 널(NaN) 값이 많이 존재하는 희소행렬이기 때문에 일반적인 SVD 방식으로 분해할 수 없고, 확률적 경사 하강법(Stochastic Gradient Descent, SGD) 이나 ALS(Alternating Least Squares) 방식을 이용해 SVD 를 수행한다.
특히, 확률적 경사 하강법을 이용한 행렬 분해를 살펴보자면 P와 Q 행렬로 계산된 예측 R 행렬 값이 실제 R 행렬 값과 최소한의 오류를 가질 수 있도록 반복적으로 비용함수를 최적화함으로써 적합한 P와 Q 행렬을 유추하는 것이 알고리즘의 골자이다.
확률적 경사 하강법을 이용한 행렬 분해의 전반적인 절차는 다음과 같다.
1. P와 Q 행렬을 임의의 값을 가진 행렬로 초기화 한다.
2. P와 Q 전치행렬을 곱해 예측 R 행렬을 계산하고, 실제 R 행렬과의 차이를 계산한다.
3. 차이를 최소화할 수 있도록 P와 Q 행렬의 값을 적절한 값으로 각각 업데이트한다.
4. 특정임계치 아래로 수렴할 때까지 2, 3번 작업을 반복하면서 P와 Q 행렬을 업데이트해 근사화한다.
실제값과 예측값의 차이 최소화와 L2 정규화(Regularization)를 고려한 비용 함수식은 다음과 같다.

위의 비용함수로 최소화하기 위해 새롭게 업데이트되는 p_new와 q_new 는 다음과 같이 계산될 수 있다. (유도는 p와 q에 대한 편미분을 통해 할 수 있다.)

4. 확률적 경사하강법(SGD) 활용예제
확률적 경사 하강법을 이용한 행렬 분해에 대한 간단한 계산 예제를 구현하면 아래와 같다.
우선, 널(NaN)값을 포함한 실제 R 행렬 및 임의의 난수로 P와 Q 행렬을 생성한다.
import numpy as np
# 원본 행렬 R 생성, 분해 행렬 P와 Q 초기화, 잠재요인 차원 K는 3 설정.
R = np.array([[4, np.NaN, np.NaN, 2, np.NaN ],
[np.NaN, 5, np.NaN, 3, 1 ],
[np.NaN, np.NaN, 3, 4, 4 ],
[5, 2, 1, 2, np.NaN ]])
num_users, num_items = R.shape
K=3
# P와 Q 매트릭스의 크기를 지정하고 정규분포를 가진 random한 값으로 입력합니다.
np.random.seed(1)
P = np.random.normal(scale=1./K, size=(num_users, K))
Q = np.random.normal(scale=1./K, size=(num_items, K))
print('실제 행렬:\n', R)
정의된 get_rmse 함수를 통해 실제 R 행렬과 예측 R 행렬과의 차이를 계산하고, 위에서 소개한 확률적 경사 하강법의 2에서 3번 과정을 1000번 반복수행하여 P와 Q 행렬을 업데이트한다. 이때 학습률은 0.01 이며, L2 정규화 계수는 0.01 로 설정하였다.
from sklearn.metrics import mean_squared_error
def get_rmse(R, P, Q, non_zeros):
error = 0
# 두개의 분해된 행렬 P와 Q.T의 내적으로 예측 R 행렬 생성
full_pred_matrix = np.dot(P, Q.T)
# 실제 R 행렬에서 널이 아닌 값의 위치 인덱스 추출하여 실제 R 행렬과 예측 행렬의 RMSE 추출
x_non_zero_ind = [non_zero[0] for non_zero in non_zeros]
y_non_zero_ind = [non_zero[1] for non_zero in non_zeros]
R_non_zeros = R[x_non_zero_ind, y_non_zero_ind]
full_pred_matrix_non_zeros = full_pred_matrix[x_non_zero_ind, y_non_zero_ind]
mse = mean_squared_error(R_non_zeros, full_pred_matrix_non_zeros)
rmse = np.sqrt(mse)
return rmse
# R > 0 인 행 위치, 열 위치, 값을 non_zeros 리스트에 저장.
non_zeros = [ (i, j, R[i,j]) for i in range(num_users) for j in range(num_items) if R[i,j] > 0 ]
steps=1000
learning_rate=0.01
r_lambda=0.01
# SGD 기법으로 P와 Q 매트릭스를 계속 업데이트.
for step in range(steps):
for i, j, r in non_zeros:
# 실제 값과 예측 값의 차이인 오류 값 구함
eij = r - np.dot(P[i, :], Q[j, :].T)
# Regularization을 반영한 SGD 업데이트 공식 적용
P[i,:] = P[i,:] + learning_rate*(eij * Q[j, :] - r_lambda*P[i,:])
Q[j,:] = Q[j,:] + learning_rate*(eij * P[i, :] - r_lambda*Q[j,:])
rmse = get_rmse(R, P, Q, non_zeros)
if (step % 50) == 0 :
print("### iteration step : ", step," rmse : ", rmse)
이렇게 분해된 P와 Q 행렬을 내적하여 예측 행렬을 만들 수 있고, 실제 행렬과 비교한 결과는 아래와 같다.
pred_matrix = np.dot(P, Q.T) # P @ Q.T 도 가능
print('실제 행렬:\n', R)
print('\n예측 행렬:\n', np.round(pred_matrix, 3))
5. 행렬 분해를 이용한 개인화 영화 추천시스템 개발
앞서 나온 MovieLens의 데이터셋을 가지고 SGD 기반으로 행렬 분해를 구현하고 이를 통해 사용자에게 영화를 추천하는 시스템을 구현한다. 이때, 위에서 언급한 RMSE 계산 함수를 그대로 사용하고, SGD 기반의 행렬 분해 시 200번의 반복계산, 학습률을 0.01, L2 정규화 계수를 0.01 로 설정하고 P와 Q 행렬을 계산한다.
import numpy as np
from sklearn.metrics import mean_squared_error
def get_rmse(R, P, Q, non_zeros):
error = 0
# 두개의 분해된 행렬 P와 Q.T의 내적 곱으로 예측 R 행렬 생성
full_pred_matrix = np.dot(P, Q.T)
# 실제 R 행렬에서 널이 아닌 값의 위치 인덱스 추출하여 실제 R 행렬과 예측 행렬의 RMSE 추출
x_non_zero_ind = [non_zero[0] for non_zero in non_zeros]
y_non_zero_ind = [non_zero[1] for non_zero in non_zeros]
R_non_zeros = R[x_non_zero_ind, y_non_zero_ind]
full_pred_matrix_non_zeros = full_pred_matrix[x_non_zero_ind, y_non_zero_ind]
mse = mean_squared_error(R_non_zeros, full_pred_matrix_non_zeros)
rmse = np.sqrt(mse)
return rmse
def matrix_factorization(R, K, steps=200, learning_rate=0.01, r_lambda = 0.01):
num_users, num_items = R.shape
# P와 Q 매트릭스의 크기를 지정하고 정규분포를 가진 랜덤한 값으로 입력합니다.
np.random.seed(1)
P = np.random.normal(scale=1./K, size=(num_users, K))
Q = np.random.normal(scale=1./K, size=(num_items, K))
break_count = 0
# R > 0 인 행 위치, 열 위치, 값을 non_zeros 리스트 객체에 저장.
non_zeros = [ (i, j, R[i,j]) for i in range(num_users) for j in range(num_items) if R[i,j] > 0 ]
# SGD기법으로 P와 Q 매트릭스를 계속 업데이트.
for step in range(steps):
for i, j, r in non_zeros:
# 실제 값과 예측 값의 차이인 오류 값 구함
eij = r - np.dot(P[i, :], Q[j, :].T)
# Regularization을 반영한 SGD 업데이트 공식 적용
P[i,:] = P[i,:] + learning_rate*(eij * Q[j, :] - r_lambda*P[i,:])
Q[j,:] = Q[j,:] + learning_rate*(eij * P[i, :] - r_lambda*Q[j,:])
rmse = get_rmse(R, P, Q, non_zeros)
if (step % 10) == 0 :
print("### iteration step : ", step," rmse : ", rmse)
return P, Q
if __name__ == "__main__":
import pandas as pd
import numpy as np
movies = pd.read_csv('./movies.csv')
ratings = pd.read_csv('./ratings.csv')
ratings = ratings[['userId', 'movieId', 'rating']]
ratings_matrix = ratings.pivot_table('rating', index='userId', columns='movieId')
# title 컬럼을 얻기 이해 movies 와 조인 수행
rating_movies = pd.merge(ratings, movies, on='movieId')
# columns='title' 로 title 컬럼으로 pivot 수행.
ratings_matrix = rating_movies.pivot_table('rating', index='userId', columns='title')
P, Q = matrix_factorization(ratings_matrix.values, K=50, steps=200, learning_rate=0.01, r_lambda = 0.01)
pred_matrix = np.dot(P, Q.T)
계산된 예측 R 행렬을 쉽게 이해하기 위해 사용자ㅡ아이템 평점 행렬을 영화 타이틀을 칼럼명으로 가지는 DataFrame으로 변경하고 출력한다.
ratings_pred_matrix = pd.DataFrame(data=pred_matrix, index= ratings_matrix.index,
columns = ratings_matrix.columns)
ratings_pred_matrix.head(3)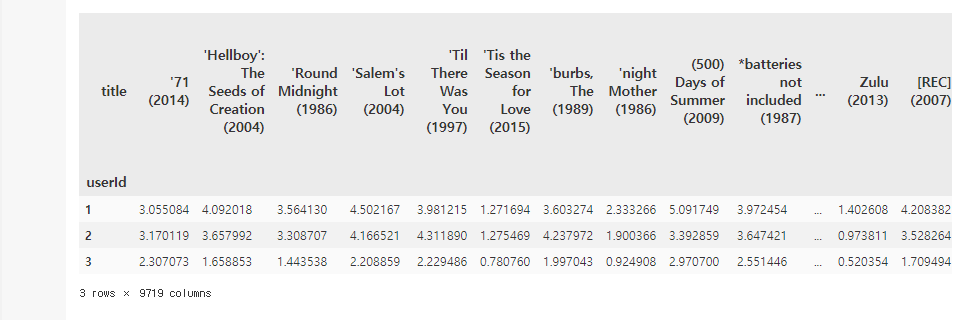
앞과 동일하게, 특정사용자가 관람하지 않는 영화만 추출해서 추천하기 위해 get_unseen_movies 함수를 작성하고, recomm_movie_by_userid 함수를 사용하여 특정사용자(user_id)의 특성에 맞춰 추천할 영화를 추출한다. 추천결과는 아래와 같다.
def get_unseen_movies(ratings_matrix, userId):
# userId로 입력받은 사용자의 모든 영화정보 추출하여 Series로 반환함.
# 반환된 user_rating 은 영화명(title)을 index로 가지는 Series 객체임.
user_rating = ratings_matrix.loc[userId,:]
# user_rating이 0보다 크면 기존에 관람한 영화임. 대상 index를 추출하여 list 객체로 만듬
already_seen = user_rating[ user_rating > 0].index.tolist()
# 모든 영화명을 list 객체로 만듬.
movies_list = ratings_matrix.columns.tolist()
# list comprehension으로 already_seen에 해당하는 movie는 movies_list에서 제외함.
unseen_list = [ movie for movie in movies_list if movie not in already_seen]
return unseen_list
def recomm_movie_by_userid(pred_df, userId, unseen_list, top_n=10):
# 예측 평점 DataFrame에서 사용자id index와 unseen_list로 들어온 영화명 컬럼을 추출하여
# 가장 예측 평점이 높은 순으로 정렬함.
recomm_movies = pred_df.loc[userId, unseen_list].sort_values(ascending=False)[:top_n]
return recomm_movies
# 사용자가 관람하지 않는 영화명 추출
unseen_list = get_unseen_movies(ratings_matrix, 9)
# 아이템 기반의 인접 이웃 협업 필터링으로 영화 추천
recomm_movies = recomm_movie_by_userid(ratings_pred_matrix, 9, unseen_list, top_n=10)
# 평점 데이타를 DataFrame으로 생성.
recomm_movies = pd.DataFrame(data=recomm_movies.values,index=recomm_movies.index,columns=['pred_score'])
recomm_movies
'인공지능 > 추천시스템' 카테고리의 다른 글
| 5. Surprise 라이브러리를 이용한 추천시스템 개발 (3) | 2021.04.10 |
|---|---|
| 3. 아이템 기반 최근집 이웃 협업 필터링 (10) | 2021.04.06 |
| 2. 콘텐츠 기반 필터링 (0) | 2021.04.06 |
| 1. 추천시스템 개요 (2) | 2021.04.06 |



