전체코드 및 결과에 대한 내용은 아래 GitHub 에 PDF 로 올려두었으니 참고해 직접 작성해보면 도움될 듯하다.
< 구현내용 >
Principal Component Analysis(PCA), 주성분 분석 알고리즘은 대표적인 비지도학습 기법으로 주로 차원을 축소하고 데이터를 압축하는데 사용되며, 알고리즘 구현방법은 아래와 같다.
- 데이터 정규화 - Whitening 이라고도 하며, 데이터분포를 원점 기준으로 변경
- Covariance matrix 의 eigen value 와 eigen vector 를 계산하고 내림차순으로 정렬
- 주성분의 수에 따라 가장 큰 n개의 eigen value를 추출하고 대응하는 eigen vector의 기저공간으로 데이터를 사영함
PCA 알고리즘 구현코드는 아래와 같다.
import numpy as np
import scipy
import scipy.stats
from sklearn.datasets import fetch_openml
import matplotlib.pyplot as plt
from ipywidgets import interact
plt.style.use('fivethirtyeight')
MNIST = fetch_openml('mnist_784', version=1)
images = MNIST['data'].to_numpy().astype(np.double) / 255.
# 1. Normalization
def normalize(X):
N, D = X.shape
mu = np.mean(X, axis=0)
Xbar = X - mu
return Xbar, mu
# 2. Covariance matrix 의 eigenvalue, eigenvector 계산
def eig(S):
eig_vals, eig_vecs = np.linalg.eig(S)
sort_indices = np.argsort(eig_vals)[::-1] # 내림차순 정렬
return eig_vals[sort_indices], eig_vecs[:, sort_indices]
# 3. Principal components 에 해당하는 각 벡터의 기저공간에 데이터 사영
def reconstruct(X, PC):
return (X @ PC) @ PC.T # vector projection 참고
# PCA 알고리즘
def PCA(images, num_components, num_data=1000):
X = images[:num_data]
N, D = X.shape
# 1. Normalization
X_normalized, mean = normalize(X)
# 2. Covariance matrix 의 eigenvalue, eigenvector 계산
S = (X_normalized.T @ X_normalized) / N
eig_vals, eig_vecs = eig(S)
# 3. Principal components 에 해당하는 각 벡터의 기저공간에 데이터 사영
principal_vals, principal_components = np.real(eig_vals[:num_components]), np.real(eig_vecs[:,:num_components])
reconst_X = reconstruct(X_normalized, principal_components) + mean
return reconst_X, mean, principal_vals, principal_components
구현예제로 MNIST 손글자 이미지데이터를 활용하여 주성분 수의 변화(1 > 30)에 따른 데이터를 살펴보았다. 아래 결과는 주성분 개수가 2, 10, 20, 30 일때 원본데이터(첫번째행)과 복원한데이터(두번째행)를 비교한 것이다.
# PCA 데이터 압축 시각화
@interact(NUM_PC=(1, 30), continuous_update=False)
def plot_pca_images(NUM_PC=15):
num_images_to_show = 10
reconst_X, _, _, _ = PCA(images, NUM_PC)
origin_image = np.reshape(images[:num_images_to_show], (-1, 28, 28))
reconst_image = np.reshape(reconst_X[:num_images_to_show], (-1, 28, 28))
fig, ax = plt.subplots(2, 1, figsize=(num_images_to_show * 3, 3))
ax[0].imshow(np.concatenate(origin_image, -1), cmap="gray")
ax[1].imshow(np.concatenate(reconst_image, -1), cmap="gray")



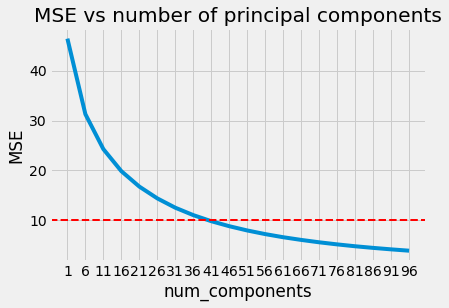
또한, 주성분 개수에 따른 원본데이터 대비 MSE 값을 계산하여 그래프를 그려보니 특정 임계치(MSE=10) 기준으로 41개 근방에서 기울기가 완만해짐을 확인할 수 있다. 따라서 데이터압축 시 41개 이하의 주성분으로도 충분히 데이터복원이 가능해질 수 있다는 것을 알 수 있다. (참고로 원본이미지 데이터의 차원수는 28 * 28 = 784 이다.)
def mse(predict, actual):
return np.square(predict - actual).sum(axis=1).mean()
loss = []
reconstructions = []
for num_component in range(1, 100, 5):
X = images[:1000]
reconst, _, _, _ = PCA(X, num_component)
error = mse(reconst, X)
reconstructions.append(reconst)
print('n = {:d}, reconstruction_error = {:f}'.format(num_component, error))
loss.append((num_component, error))
reconstructions = np.asarray(reconstructions)
reconstructions = reconstructions
loss = np.asarray(loss)
# MSE 시각화
fig, ax = plt.subplots()
ax.plot(loss[:,0], loss[:,1]);
ax.axhline(10, linestyle='--', color='r', linewidth=2)
ax.xaxis.set_ticks(np.arange(1, 100, 5));
ax.set(xlabel='num_components', ylabel='MSE', title='MSE vs number of principal components');
아래는 주성분 갯수에 따른 MNIST 데이터셋의 복원정도를 살펴본 것으로, 맨 좌측은 원본데이터, 그 다음 우측 첫번째부터 주성분 수를 5개 간격으로 증가시켜 복원한 이미지데이터이다.
@interact(image_idx=(0, 1000))
def show_num_components_reconst(image_idx):
fig, ax = plt.subplots(figsize=(20., 20.))
actual = X[image_idx]
x = np.concatenate([actual[np.newaxis, :], reconstructions[:, image_idx]])
ax.imshow(np.hstack(x.reshape(-1, 28, 28)[np.arange(10)]), cmap='gray');
ax.axvline(28, color='orange', linewidth=2)

728x90
반응형
'인공지능 > 코드구현' 카테고리의 다른 글
| Distance & Angle을 활용한 이미지 유사도 계산 (6) | 2021.05.25 |
|---|---|
| 구글의 페이지랭크(PageRank) 알고리즘 (14) | 2021.04.12 |
| 벡터 선형 변환을 통한 이미지 축변환 (대칭/회전) (1) | 2021.04.08 |


