전체코드 및 결과에 대한 내용은 아래 GitHub 에 PDF 로 올려두었으니 참고해 직접 작성해보면 도움될 듯하다.
< 구현내용 >
이미지 벡터간 유클라디언 거리 또는 내각 계산을 활용하여 이미지간 유사도를 찾는 실험을 수행하였는데, 그 내용은 다음과 같다.
- 이미지벡터간 거리비교
- 거리기반 가장 유사한 이미지 도출
- MNIST 클래스별 유사성 비교
아래는 MNIST 데이터셋의 거리를 활용하여 유사성을 계산한 코드이며 세부 실험별 내용은 아래와 같다.
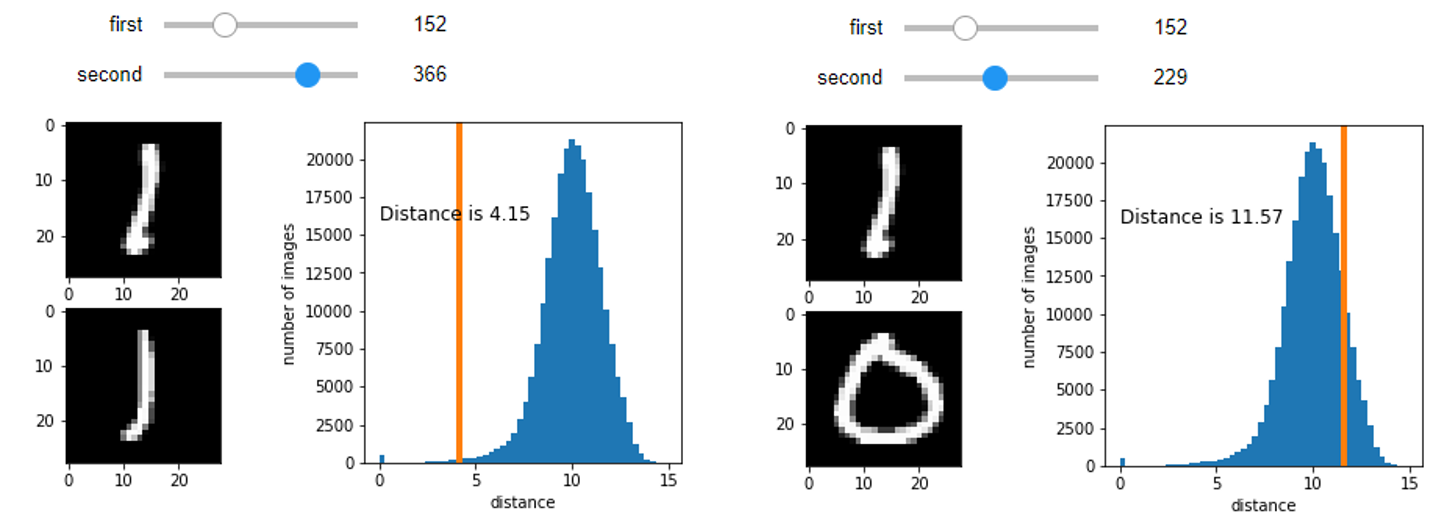
(1) 이미지벡터간 거리비교
직관적으로 같은 클래스 내의 이미지일수록 혹은 유사한 이미지일수록 거리값이 낮은 것을 확인할 수 있다.
import numpy as np
import matplotlib.pyplot as plt
from ipywidgets import interact
from sklearn.datasets import fetch_openml
# MNIST 데이터셋 다운로드
MNIST = fetch_openml('mnist_784', version=1)
images = MNIST['data'].to_numpy().astype(np.double) / 255. # 정규화는 안해도 됨
labels = MNIST['target'].to_numpy().astype(np.int)
# 이미지 벡터간 거리계산
def distance(x0, x1):
x = x0 - x1
distance = np.sqrt(x @ x)
return distance
# 이미지 벡터간 각도계산
def angle(x0, x1):
nominator = x0@x1
denominator = np.sqrt((x0@x0)*(x1@x1))
angle = np.arccos(nominator/denominator)
return angle
# 500장 이미지 벡터간 거리비교
distances = []
for i in range(len(images[:500])):
for j in range(len(images[:500])):
distances.append(distance(images[i], images[j]))
@interact(first=(0, 499), second=(0, 499), continuous_update=False)
def show_img(first, second):
plt.figure(figsize=(8,4))
f = images[first].reshape(28, 28)
s = images[second].reshape(28, 28)
ax0 = plt.subplot2grid((2, 2), (0, 0))
ax1 = plt.subplot2grid((2, 2), (1, 0))
ax2 = plt.subplot2grid((2, 2), (0, 1), rowspan=2)
ax0.imshow(f, cmap='gray')
ax1.imshow(s, cmap='gray')
ax2.hist(np.array(distances), bins=50)
d = distance(f.ravel(), s.ravel())
ax2.axvline(x=d, ymin=0, ymax=40000, color='C1', linewidth=4)
ax2.text(0, 16000, "Distance is {:.2f}".format(d), size=12)
ax2.set(xlabel='distance', ylabel='number of images')
plt.show()
(2) 거리기반 가장 유사한 이미지 도출
계산된 거리를 이용해서 가장 유사한 이미지의 인덱스값을 반환받아 실제로 정말 유사한지 비교해보니, 얼핏보면 거의 같은 이미지라고 생각될 수 있을정도로 유사한 것으로 확인할 수 있다.
# 가장 가까운 거리의 이미지 인덱스 찾기
def most_similar_image(idx):
distances = np.zeros((500))
for i in range(500):
distances[i] = distance(images[idx], images[i])
idx = np.where(distances == sorted(distances)[1])[0] # 자기 자신은 제외
return idx
@interact(idx=(0, 499), continuous_update=False)
def show_most_similar(idx):
plt.figure(figsize=(8,4))
f = images[idx].reshape(28, 28)
similar_idx = most_similar_image(idx)
s = images[similar_idx].reshape(28, 28)
ax0 = plt.subplot(1,2,1)
ax1 = plt.subplot(1,2,2)
ax0.imshow(f, cmap='gray')
ax0.set_title('original')
ax1.imshow(s, cmap='gray')
ax1.set_title('most_similar')
plt.show()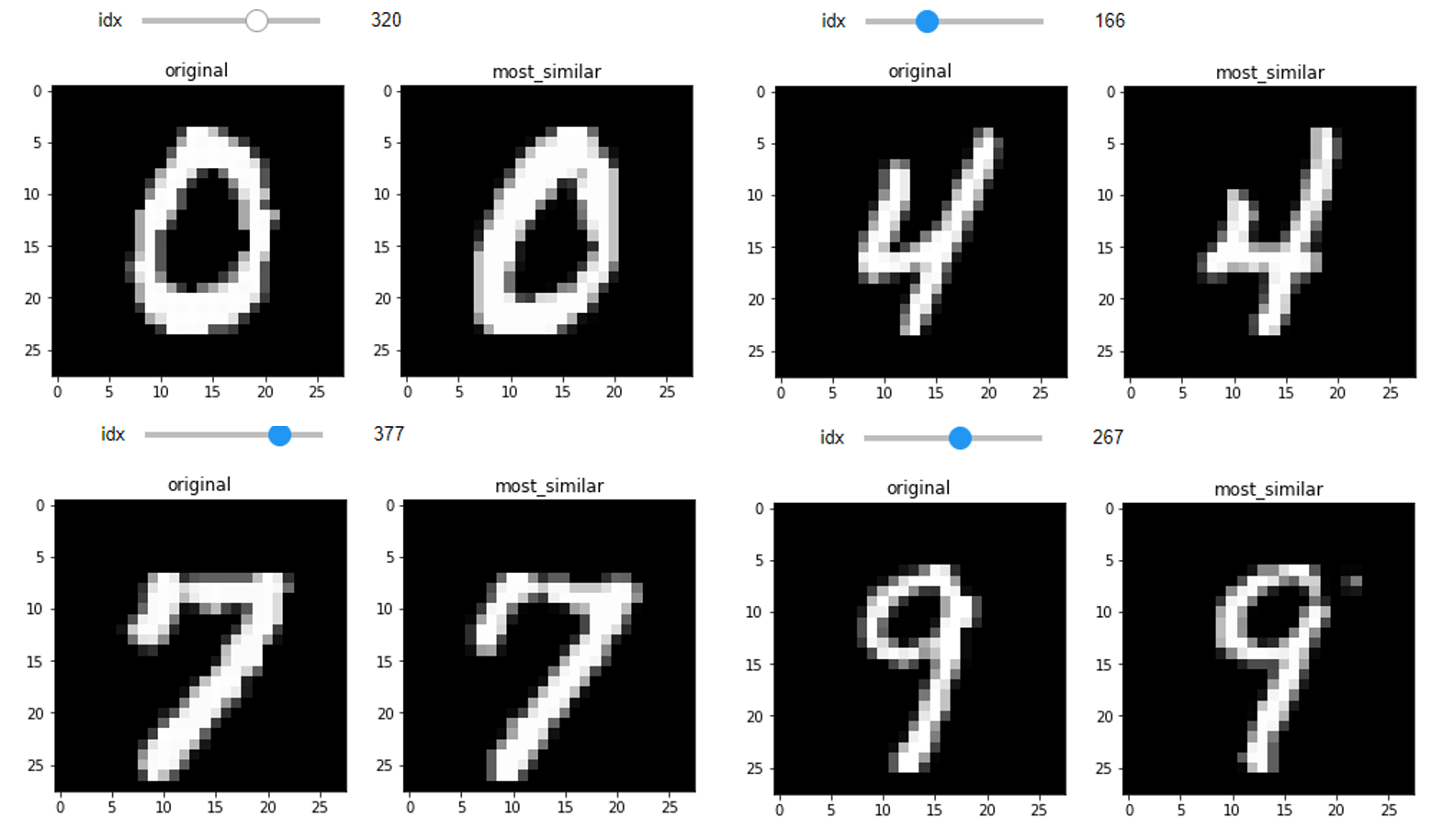
(3) MNIST 클래스별 유사성 비교
클래스별 평균을 가지고 유사도를 비교했을 때 어느 클래스끼리 비슷한지 확인할 수 있고, 여기서는 거리기반보다 벡터간 각도를 통해 유사도(코사인유사도)를 계산한 것이 기대했던 바와 더 근사했다. 아래는 거리 기반으로 평가한 결과를 시각화한 내용이다.
# 클래스별 유사도 비교
mean_images = {}
for n in np.unique(labels):
mean_images[n] = np.mean(images[labels==n], axis=0)
MD = np.zeros((10, 10))
AG = np.zeros((10, 10))
for i in mean_images.keys():
for j in mean_images.keys():
MD[i, j] = distance(mean_images[i], mean_images[j])
AG[i, j] = angle(mean_images[i].ravel(), mean_images[j].ravel())
# 결과 시각화
fig, ax = plt.subplots(figsize=(8,8))
grid = ax.imshow(MD, interpolation='nearest')
ax.set(title='Distances between different classes of digits',
xticks=range(10),
xlabel='class of digits',
ylabel='class of digits',
yticks=range(10))
fig.colorbar(grid)
plt.show()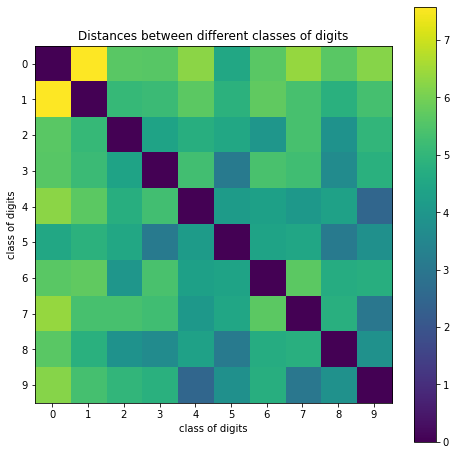
728x90
반응형
'인공지능 > 코드구현' 카테고리의 다른 글
| Principal Component Analysis(PCA) 알고리즘 (15) | 2021.05.27 |
|---|---|
| 구글의 페이지랭크(PageRank) 알고리즘 (14) | 2021.04.12 |
| 벡터 선형 변환을 통한 이미지 축변환 (대칭/회전) (1) | 2021.04.08 |


