< 목차 >
- 용어정의
- Multivariate analysis : PCA (2/2)
- Principal component analysis (PCA in details)
1. 용어정의
아래 페이지를 참고해주세요.
2. Principal component analysis (PCA in details)
2021.04.01 - [인공지능/머신러닝] - 4-1. Multivariate Analysis : PCA (1/2) 의 글에서 소개된 PCA 알고리즘을 수식으로 하나씩 풀어나려면, 우선 데이터 X에 대한 Covariance matrix 계산이 필요하다.
기존의 입력데이터 X가 m > n인 m x n 의 차원크기를 갖는다면, 각 요소들에 대한 공분산(Covariance)는 아래 수식으로 전개되어 m x m 의 정방형 행렬로 존재한다.

이후, C_x의 Covariance matrix를 eigenvalue problem 에 대입하여 해석하면 아래와 같이 전개될 수 있다.

위의 수식에서 'λ'는 eigenvalue이며 'E'는 λ에 대응하는 eigen vector, 'i'는 C_x 차원의 크기인 m의 크기를 가진다. 이때, λ는 대각행렬로써 E의 뒷부분에 위치해도 동일하고, 여기서 λ의 각 요소는 첫번째부터 m번째까지 그 크기가 점점 작아지는 순서로 위치한다고 가정한다.
이러한 λ를 D라는 행렬로 표현하고, 이때 eigen vector인 E가 orthonormal 하다면, 다음과 같은 성질을 가지고 아래의 성질로 인해 C_x는 E와 D의 행렬로 위에 설명된 마지막 수식과 같이 표현될 수 있다.

이때, 행렬 C_y는 C_x와 마찬가지로 Y에 대한 행렬로 표현되며, Y = PX 라고 가정한다면 아래의 수식과 같이 전개될 수 있다. 또한, P = transposed(E) 일 때, X 행렬에 관한 항을 C_x로 표현하고 앞서 구했던 E와 D에 대한 행렬로 다시 표현한다면 C_y 또한 E와 D에 대한 행렬로 나타난다. 마지막으로 이러한 행렬은 orthonormal 한 성질에 의해 eigenvalue가 있는 D 행렬만 남겨지게 된다.

위의 수식으로 살펴본 PCA의 장단점은 아래와 같다.
- 장점
- Non-parametric mapping : 특정분포를 가정하고 평균과 분산에 대해 매개변수를 추정할 필요가 있던 회귀분석과 같은 Parametric mapping와 달리 추정할 매개변수 없이 행렬연산으로 계산이 이루어진다.
- Feature extraction method : 입력데이터에서 필요한 정보에 대한 특징을 추출할 수 있다.
- Unsupervised method : 입력데이터 X에 대해 타겟값(Label)이 필요없다.
- Data reduction method : 각 주성분이 orthonormal 하여 불필요한 정보를 최소화한다.
- Noise reduction method : 위와 동일한 의미를 갖는다.
- Reveal hidden structure : 불필요 정보를 제거하여 가려진 데이터의 정보를 획득할 수 있다.
- Y becomes closer to a Gaussian distribution : i.i.d 한 데이터는 주성분 축을 기준으로 Central limit theorem을 따라 정규분포형태를 띄게 된다.
- 단점
몇 가지 가정을 하고 PCA 연산을 수행하기 때문에, 실제데이터와 가정이 다를 경우 PCA 방법은 효과적이지 않다.
- Linear mapping : Y = PX 의 규칙을 통해 선형적으로 축변환이 일어난다.
- Sorting based on entropy(Variance) : eigenvalue problem에서 λ 의 값이 크기가 큰 순서대로 존재한다.
- P matrix is orthonormal : 주성분 P행렬과 해당 전치행렬의 내적은 Identity matrix이다.
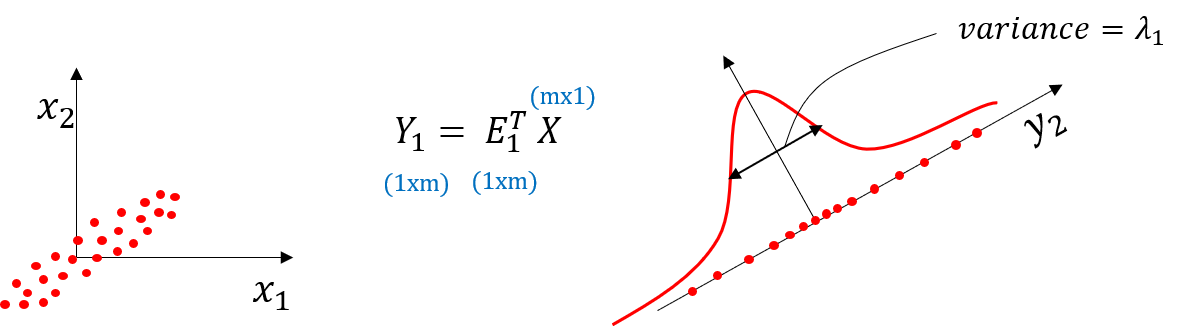
아래 두 가지 그림은 PCA 의 한계를 설명해준다.
<A 그림> : 위와 같은 3차원에서의 데이터 분포는 비선형적(원형의 빨간 점선)의 축이 가장 분산이 큰 축이지만, PCA를 적용했을 때 직각성분(선형)의 축을 주성분으로 나타내므로, 가장 분산이 큰 축을 나타낼 수 없다. 이를 극복하기 위해서, Non-linear PCA 가 존재한다.
<B 그림> : 2차원 데이터 분포에서 PCA를 적용했을 때 각 축은 수직(orthogonal)을 이루어야 하지만, 아래그림에서 실제로 가장 분산이 큰 두 개의 축은 수직이 아닐 수 있다. 따라서 PCA를 적용하는데 효과적이지 못하다. 그리고 실제로는 이러한 경우가 다수 존재한다.

'인공지능 > 머신러닝 이론' 카테고리의 다른 글
| 4-4. Factor Analysis (FA) (0) | 2021.04.02 |
|---|---|
| 4-3. Independent Component Analysis (ICA) (0) | 2021.04.02 |
| 4-1. Multivariate Analysis : PCA (1/2) (0) | 2021.04.02 |
| 3-9. Iterative Reweighted Least Squares (0) | 2021.04.01 |
| 3-8. Logistic Regression (0) | 2021.04.01 |



