< 목차 >
- 용어정의
- Factor analysis (FA)
- Understanding of FA
1. 용어정의
아래 페이지를 참고해주세요.
2. Factor analysis (FA)
관측된 데이터 X는 어떠한 상호의존적인 미지수(F)와 미소한 오차성분(ε)에 의한 선형결합으로 나타난다고 보면, 반대로 우리는 어떤 요소들이 관측데이터 X에 대해 얼마나 큰 영향을 주는지 확인할 수 있다.
예로 들면 X인 수학, 과학, 영어의 점수가 알려지지 않은 요소인 F(Common factors), 즉 I.Q, 학습시간, 학습빈도 등의 여러가지 요인과 가중치 L(Loading matrix)의 결합으로 표현될 수 있고 이러한 F와 L을 구하여 각 요소가 미치는 영향을 파악할 수 있다.

Common factor와 Loading matrix 를 구하기위해 아래의 전제를 기본으로 하며,

그러면 관측데이터 X의 분산인 C_x는 아래와 같이 나타날 수 있다.

또한, X와 F에 대한 분산은 위의 수식에 따라 다음과 같이 나타난다.

또한, 위의 전제에 따라 각 요인들이 얼마만큼 강력한 상관관계를 갖는지 비교할 수 있는데 이를 Loading Estimation Method 라고 하며, 아래와 같이 설명될 수 있다.

p개의 관측데이터 X에 대한 p x p 차원크기의 분산은 eigenvalue(D)와 eigen vector(E)로 전개되며, Loading matrix(L)와 Error를 나타내는 Variance로 표현될 수 있으며, Error = 0 일 경우에 L의 내적으로 나타난다. 이어서, 만약 관측데이터의 개수 p가 임의로 정한 m의 크기보다 클 경우에 m번째 eigenvalue와 이에 상응하는 eigenvector를 이용해서 관측데이터 X에 대한 분산을 다시 구할 수 있다.

이때 m에 따라서, 다시 구한 분산이 전체 관측데이터 중 어느정도 수준으로 각 요인들의 상관관계를 설명할 수 있는지 달라지며, 최적의 m을 선택하는 기준은 아래의 세 가지 방법이 있다.

마찬가지로, 반대로 이항하여 Error인 Variance(φ)에 대하여 구할수도 있다.
3. Understanding of FA
설명이 조금 어려울 수 있어서 간단한 예제를 통해 이해를 돕자면, 소비자 선호도 조사를 통해 새로운 상품의 선호도 조사를 들 수 있다.
아래 도표는 (1) 맛, (2) 경제성, (3) 향기, (4) 스낵으로서 적절성, (5) 공급에너지의 다섯가지 지표의 상관관계(R)이며, 해석하면 (1) 맛은 (3) 향기와 크게 연관이 있고 (5) 공급에너지는 (2) 경제성과 (3) 스낵으로서 적절성과 다소 연관이 있는 것으로 해석할 수 있다.

이때 위의 도표로 eigenvalue를 구하고, R이 1이상인 기준으로 m = 2로 선택하였다. 그리고 누적된 부분에 대해 정규화하면 다음과 같은 값이 나오는데, 이는 전체데이터 X 중 93%를 두 개의 eigenvalue로 재구축한 Correlation(R)으로 표현할 수 있다는 것이다.

미리 주어진 Common Factor를 통해서 관측데이터 X에 대한 상관관계를 다시 재구축하면 아래와 같다.
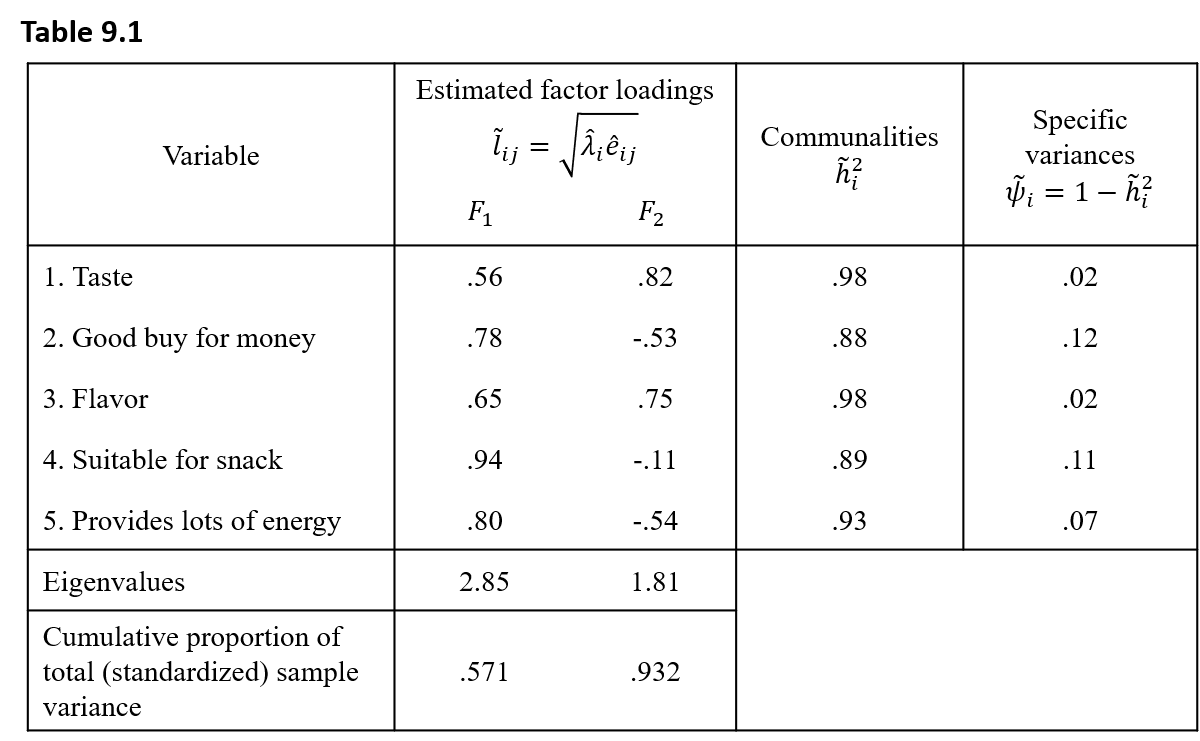

이제 반대로, Common Factor 를 구하기 위해서는 맨 위에서 설명한 것과 같이 관측데이터 X는 L과 F, 그리고 Error(ε)의 선형결합으로 다음과 같이 표현할 수 있다.

또한, Error를 최소화하기 위한 Objective Function은 아래와 같으며, 이를 최소화하는 F를 구하면 다음과 같이 전개된다.

여기서,unweighted least squares 방법과 L이 eigenvalue problem 을 이용해서 얻어졌다는 사실을 이용하면, Common Factor인 F는 다음과 같이 간단하게 나타낼 수 있다.

이로써, 우리는 불필요한 정보를 무시하고 영향력이 큰 eigenvalue와 그로 인해 얻어지는 Loading matrix, Common factor을 구해서 보다 명료하게 지표별 상관관계를 분석할 수 있다.
'인공지능 > 머신러닝 이론' 카테고리의 다른 글
| 5-1. Introduction to Neural Networks (0) | 2021.04.03 |
|---|---|
| 4-5. Projection Pursuit (PP) (0) | 2021.04.02 |
| 4-3. Independent Component Analysis (ICA) (0) | 2021.04.02 |
| 4-2. Multivariate Analysis : PCA (2/2) (0) | 2021.04.02 |
| 4-1. Multivariate Analysis : PCA (1/2) (0) | 2021.04.02 |



