< 목차 >
- 용어정의
- Mixtures of Gaussians
- EM algorithm for Gaussian mixtures
- Comparison of EM algorithms
1. 용어정의
- 피드백 후 작성예정입니다.
2. Mixtures of Gaussians
가우시안 혼합 분포(Mixtures of Gaussians)은 복수의 가우시안 분포들의 선형 결합으로 실제데이터의 분포를 근사하는 방법으로 아래와 같은 그림으로 표현할 수 있다.
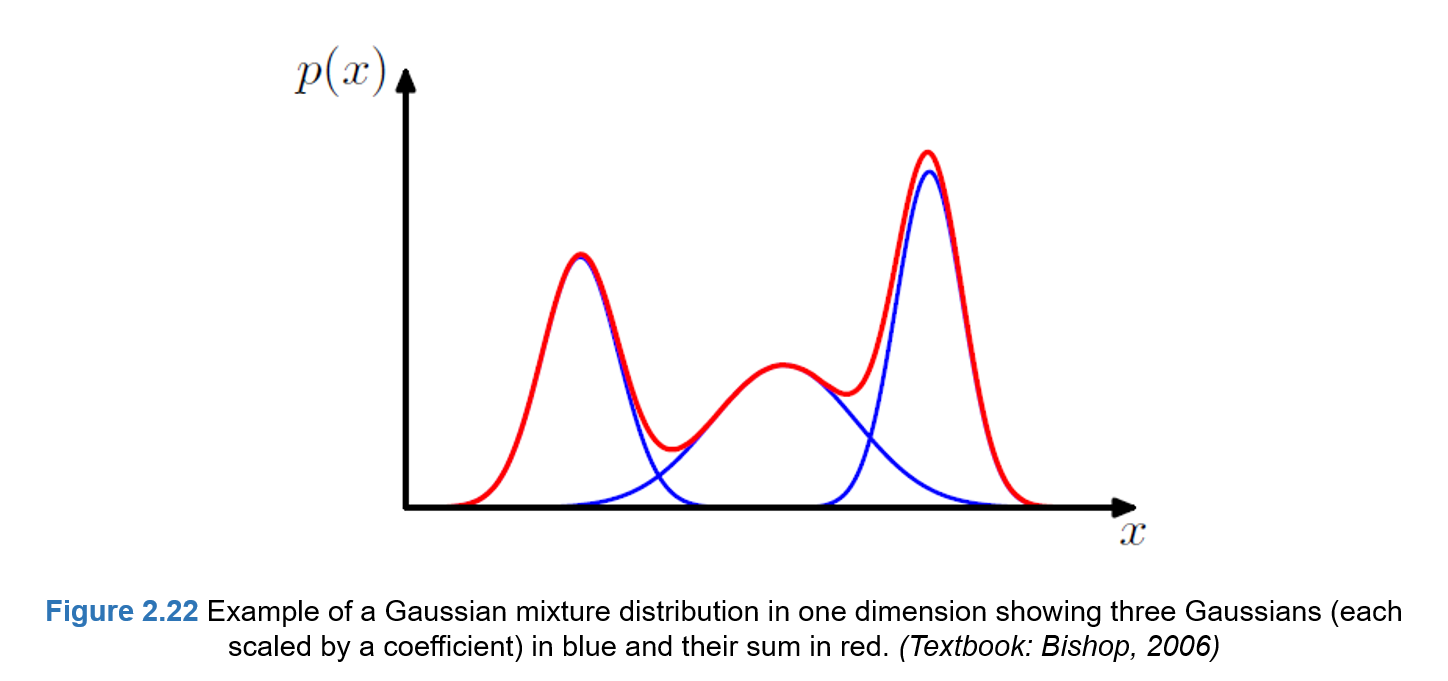
이는 아래 오른쪽 그림과 같이, 단일 가우시안 분포를 통해 데이터 분포를 표현하기엔 한계가 존재하고 복수의 혼합 분포를 사용해서 더 정확하게 표현할 수 있기 때문에 유용하게 사용되는 방법이다.

즉, 가우시안 혼합분포를 나타내기 위해서는 잠재변수(Latent variable)인 'z' 를 사용하며, 아래와 같은 확률분포 모델로 표현할 수 있다.
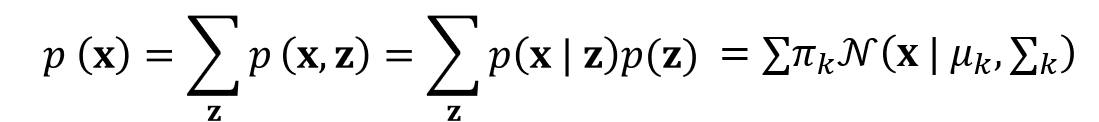
이때, z는 K크기의 차원을 갖는 "Binary"의 랜덤변수이며, one-hot-encoding과 동일한 형식으로 표현되고 총합은 '1' 이다.

또한, 잠재변수 z에 대한 확률분포 p(z)는 z_k = 1일 때, π_k로 표현된다.

즉, 입력데이터의 확률분포 p(x) 는 π_k 과 적절한 평균과 분산을 갖는 복수의 가우시안 분포모델에 대한 선형결합으로 표현될 수 있다. 그러므로 이론적으로는 어떠한 연속적인 확률밀도 함수라도 가우시안 혼합분포 모델을 이용해서 나타낼 수 있다.

이때 각각의 단일 가우시안 분포는 잠재변수 z에 대한 조건부 확률밀도 모델 p(x|z)로 나타낼 수 있고, p(z_k = 1)인 경우에 대한 posterior probability인 γ(z_k)는 다음과 같이 베이지안 방법을 통해 나타낼 수 있다.
그리고 이것은 z_k=1인 k번째 가우시안 확룰분포가 관측데이터 x를 설명할 수 있다는 것을 의미한다.

3. EM algorithm for Gaussian mixtures
D크기의 차원을 가진 N개의 데이터가 있고, 잠재변수 z가 K 크기의 차원을 갖고 데이터의 수와 동일하게 N개 있다고 가정하면, Likelihood method을 이용해서 p(x)를 최대화하는 'μ_k', 'π_k' 와 '∑_k' 을 추정하는 것이다. 이때, 계산편의를 위해 p(x)에 Logarithm을 취하고, 'μ_k', 'π_k' 와 '∑_k' 를 임의 값으로 설정한다.

EM algorithm을 이용하여 가우시안 혼합분포 모델을 추정하는 방법은 위와 마찬가지로 Expectation-Maximization 의 Two-step을 따른다.
(1) Expectation step
- p(z_k = 1)인 경우에 대한 posterior probability인 γ(z_k)을 추정한다.

(2) Maximization step
- γ(z_k) 을 고정한 채로, p(x)를 최대화하는 'μ_k', 'π_k' 와 '∑_k' 를 계산하고, ln(p(x)) 가 수렴하는데 까지 E-M 과정을 반복한다.

아래는 EM algorithm 을 이용해서 가우시안 혼합분포 모델을 실제데이터 분포에 맞게 근사한 결과이며 'L'은 E-M 과정의 반복횟수를 나타낸다. 여기서 반복횟수가 증가할수록 가우시안 혼합모델이 데이터의 분포를 점점 더 정확하게 표현할 수 있음을 확인할 수 있다.

4. Comparison of EM algorithms
7장에서는 EM algorithm을 이용하여 K-means clustering 과 Gaussian mixtures 모델을 관측데이터에 적용하는 방법을 설명했다. 이때 두 가지 모델의 차이점은 아래와 같이 요약될 수 있다.

'인공지능 > 머신러닝 이론' 카테고리의 다른 글
| 7-2. EM algorithm for K-means clustering (2) | 2021.04.05 |
|---|---|
| 7-1. Mixture Models and Expectation-Maximization(EM) Algorithm (0) | 2021.04.05 |
| 6-4. Classification of a new data point (0) | 2021.04.05 |
| 6-3. Quadratic Optimization Problem (0) | 2021.04.05 |
| 6-2. Margin of Support Vector Machine(SVM) (2) | 2021.04.05 |



