< 목차 >
- 용어정의
- Overview of MLP
- Regression vs. Classification
- Issues for neural network construction
1. 용어정의
- 패드백 후 작성 예정입니다.
2. Overview of MLP
Mulit-Layer Perceptron(MLP) Neural Network 는 말그대로 다수의 레이어로 구성된 네트워크로 아래의 구조와 같이 Input Layer, Hidden Layer, Output Layer 로 구성된다.
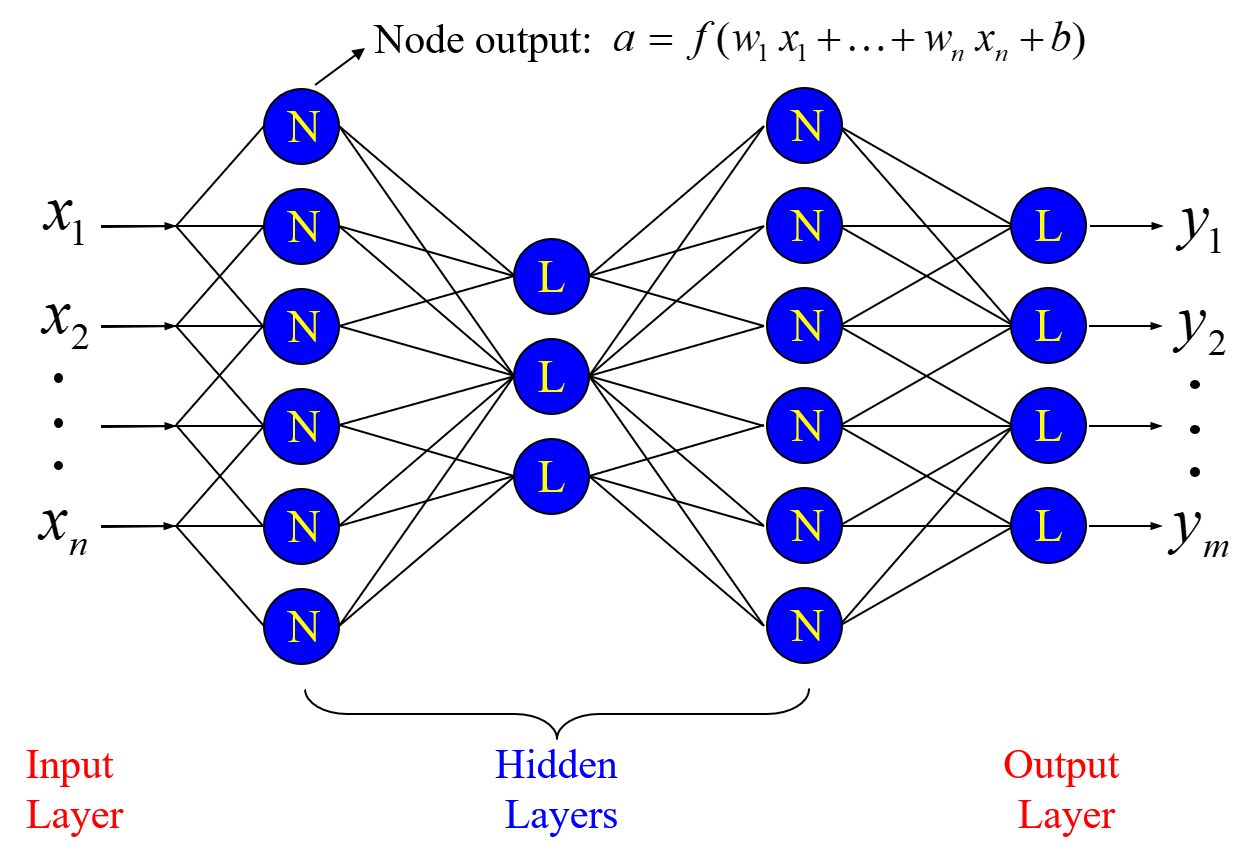
MLP의 연산과정을 구체적으로 살펴보면, 다음 순서로 나타난다.
(1) Input layer에서 입력된 각 데이터들은 각 노드와 노드를 연결하는 Weight를 통해 가중된다.
(2) h( ) 함수를 통해 변환되어 Hidden layer의 입력 값(z)으로 전달된다. 이때, Hidden layer에 존재하는 h( ) 함수로는 주로 'Logistic sigmoid unit' 이나 'tanh unit' 을 사용한다.
(3) 같은 방식으로 Output layer와 연결된 Weight 를 통해 가중되며 마지막으로 f( ) 함수를 통해 변환되어 출력된다. 이때, f( ) 함수로는 Regression 일 경우 그대로 출력하고, 0과 1의 two-classes 를 갖는 Binary classification 일 때는 Sigmoid units, Multi-class의 경우 Softmax function을 만난다.

3. Regression vs. Classification
앞서 설명했듯 뉴럴 네트워크는 Regression 혹은 Classification 문제에 따라 사용되는 함수가 달라진다.
Regression의 경우 출력값 y를 특정 함수에 근사하도록 하여 출력층에서 별도의 함수를 사용하지 않는다. 반대로, Classification 에서는 [0, 1] 범위 내에서 각 클래스에 대해 이진화(binarization)가 이루어져야 하기 때문에 마지막에 [0, 1] 로 압축시켜줄 함수가 필요하다. 그렇기 때문에 Classification 문제에서는 출력부에 Sigmoid units을 사용한다.

이러한 두 가지 경우를 모두 고려해 간단한 포맷으로 나타낸 수식이 바로 아래의 경우이다.

또한, 위의 수식은 Bias 항을 고려하여 명시적(explicit) 혹은 묵시적(implicit)한 포맷을 나타낼 수도 있다.

4. Issues for neural network construction
뉴럴 네트워크의 원리를 이해하고 이를 설계할 때, 반드시 고려해야할 요소가 있다.
(1) INPUT / OUTPUT SELECTION
- 입력데이터로 어떤 값을 사용할지, 그리고 네트워크가 학습해야할 타겟데이터는 어떤 값을 사용해야 하는지는 굉장히 중요하다.
- 특히 입력데이터를 고려하는 과정에서는 Feature extraction이 전처리과정으로 적용되는 경우가 많은데, 하나의 예로 들자면 상관관계가 높은 지표를 굳이 입력데이터로 사용해서 네트워크의 연산로드를 높일 필요가 없기 때문이다. 그렇기 때문에 적절한 입력데이터를 분석하고 정제할 수 있는 역량이 매우 중요하다고 볼 수 있다.
(2) SELECTION OF NETWORK ARCHITECTURE
- 네트워크의 구조 또한 기본적으로 고려해야할 요소가 있다.
- Hidden layer 의 수는 몇 개의 층으로 구성할 것인가?
- 각 레이어에서 Neurons (nodes) 의 숫자는 얼마나 둘 것인가?
- Activation function은 어떤 unit 으로 사용할 것인가?
(3) OBJECTIVE FUNCTION / OPTIMIZATION
- 마지막으로 설계한 네트워크가 학습하기 위해, 즉 error를 최소화 하기 위한 Objective function을 정의해야할 필요가 있다.
- 또 정의한 Objective function에 따라 어떠한 방식의 Optimization (혹은 Backpropagation) 방법을 사용할 것인지도 정의해야 한다. Optimization 방법은 아래 수식의 Descent Gradient 방식을 기반으로 하여 Stochastic Descent Gradient, Momentum, RMS Prop, AdaM 등 다양하게 존재한다.

728x90
반응형
'인공지능 > 머신러닝 이론' 카테고리의 다른 글
| 5-4. Radial Basis Function(RBF) Neural Network (0) | 2021.04.04 |
|---|---|
| 5-3. Network Training (0) | 2021.04.03 |
| 5-1. Introduction to Neural Networks (0) | 2021.04.03 |
| 4-5. Projection Pursuit (PP) (0) | 2021.04.02 |
| 4-4. Factor Analysis (FA) (0) | 2021.04.02 |



