< 목차 >
- 용어정의
- Error functions
- Neural network parameter estimation
- Error backpropagation
- Convergence and local minima
- Generalization for neural network
1. 용어정의
- 피드백 후 추가 예정입니다.
2. Error functions
뉴럴네트워크 가중치의 학습을 위해서는 타겟데이터와 연산된 출력값 간의 오차가 최소화되도록 하는 Objective function 의 정의가 필요하며, Regression 과 Classification 문제에 따라 Objection function은 달라진다.
(1) Regression
- 회귀(Regression) 문제는 네트워크 연산을 통해 나온 출력값 y 와 타겟데이터 t 간의 오차를 보는 것으로 아래 수식을 따른다.

(2) Binary Classification
- '0'과 '1'의 두 개의 클래스로만 나타나는 Binary Classification 문제에서는 0과 1의 범위로 제한하는 Logistic sigmoid function을 사용하며, Cross-Entropy 수식을 따른다.

(3) Multi-class Classification
- 다수의 클래스로 분류하는 Classification 문제에서는 위와 동일하게 Cross-Entropy 수식을 따르며, 모든 출력값의 총합이 '1'이 되도록하는 Softmax function을 사용한다.

3. Neural network parameter estimation
뉴럴 네트워크가 학습하는 원리는 각 문제에 맞는 Objective function을 사용하여 이를 최소화할 수 있는 가중치를 매번 갱신(update)하여 타겟데이터와 최대한 근사한 값을 출력하는 것이다.
아래 그림은 Objective function인 E(w)을 가중지 w1과 w2 에 대해 3차원 그래프로 시각화한 것이다.
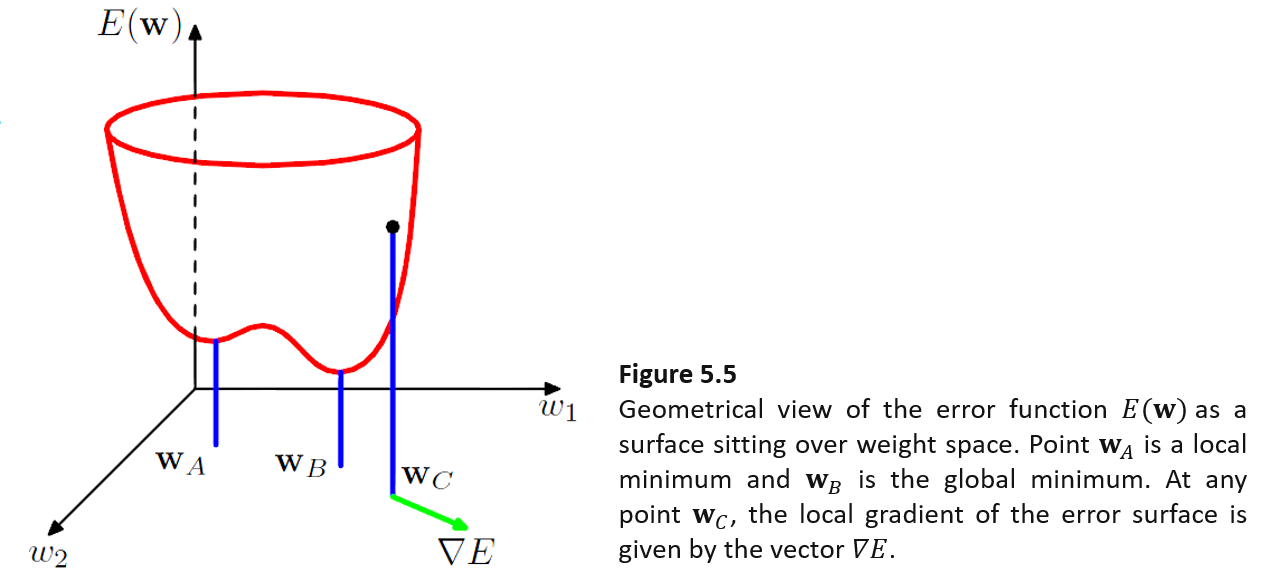
그래프를 보면 w_C에서 ▽E 의 반대방향으로 점차 w 벡터를 이동시키며, w_A 나 w_B 값으로 접근할 수 있음을 알 수 있다. 위를 내용을 일반적인 수식으로 전개하면 아래와 같다.

▽E 의 반대방향으로 학습률(Learning rate)의 크기에 따라 조금씩 이동하면서 E(w)가 최소가 되는 최적의 'w'값을 찾기 때문에 이를 역전파, 즉 'Backpropagation' 이라고 한다.
4. Error backpropagation
역전파(Backpropagation)의 목표는 ▽E(w) 의 크기나 방향을 평가하여 네트워크의 가중치인 w를 학습시키는 것이다. 간단한 예제로 Regression 문제를 풀기 위한 세 개의 레이어를 갖는 뉴럴네트워크의 연산과정을 살펴보면 다음과 같이 이해할 수 있다.

< Forward >
① n개의 타겟데이터에 대한 E(w) 의 합을 구한다.
② 여기서 임의의 n번째 타겟데이터에 대한 E(w) 값은 출력값 간의 차이이다.
③ 출력값(y_k)은 두번째 레이어(j)의 출력값(z_j)를 입력으로 받고 두번째 레이어와 세번째 레이어(k) 사이를 잊는 가중치(W_kj) 와 곱을 통해 계산된다.
< Backward >
④ E(w)를 가중치(w_kj)에 관해 편미분하는데, 이것은 해당 가중치에 따른 E(w)의 변화률을 확인하는 의미로 해석할 수 있고, Chain Rule 을 통해 아래의 수식으로 전개된다.
⑤ 동일한 방식으로 E(w)를 가중치(w_ji)에 대해 편미분하며, Chain Rule에 의해 아래와 같이 나타날 수 있다.
위의 순서를 단계적으로 구현하기 위해 설명하면 아래와 같다.
(1) 가중치를 난수로 생성한다.
(2) n개의 입력데이터 X를 네트워크에 넣어 n개의 출력데이터 Y를 계산한다.

(3) n번째 데이터에서 출력값과 타겟값 간의 차이인 δ (error) 을 계산한다.

(4) 각 가중치에 대한 E(w)의 변화률을 구하기위해 각 레이어에서 각 가중치를 각각의 δ 에 곱해준다.

(5) 모든 n번째 데이터에 대해서 (2)번부터 반복하여 E(w)의 변화율을 구하고, 모든 n에 대한 총합을 구한다.

(6) 가중치 'w' 를 업데이트 한다.

결과적으로, 위의 역전파(Backpropagation) 방식을 수차례 반복하여 최적의 가중치 값을 찾으며, 적은 수의 반복학습은 출력데이터와 타겟데이터 간의 오차를 감소시키는데 충분하지 않고(underfitting), 반대로 너무 많은 반복학습은 네트워크의 과적합(overfitting)을 발생시킨다.
따라서 얼마나 반복해야하는지 반복횟수를 사전에 정의하는 것이 반드시 필요하며, 기본적으로 아래의 세 가지 방법을 사용할 수 있다.
- 학습 전에 몇번 반복할 것인지 미리 정해놓는 방법 (예, Epoch = 1000)
- 사전에 정해놓은 임계값 이하로 E(w)가 감소하였을 때 학습을 완료하는 방법
- 학습과정에서 검증을 주기적으로 실행하여, 특정 기준을 만족하는 경우 학습을 완료하는 방법
5. Convergence and local minima
E(w) 평면을 시각적으로 표현해보면, E(w)의 미분값이 0이 되는 다수의 Local minima 가 존재하고 모든 E(w)평면에서 최소가 되는 Global minima 가 아닌 Local minima에 수렴하게 되는 경우도 있다.
하지만 Local minima 에 수렴하는 가중치 w가 뉴럴네트워크의 성능에 크게 영향일 미치는 것은 아닐 뿐더러, E(w)를 최소화하는 가중치 w가 Local minima 인지 Global minima 인지 확인할 수 있는 방법이 없다. 따라서, 아래의 heuristic한 방법을 이용해서 Local minima 을 피하는 방법을 사용한다.
(1) Momentum을 가중치 w을 업데이트할 때 추가하는 방법
- Momentum을 이용하는 것은 바로 직전에 업데이트된 w의 방향과 크기를 현재시점에도 고려하여, Local minima에 빠지지 않도록 하는 것이다.

(2) Stochastic Gradient Descent 를 사용하는 방법
- (True) Gradient Descent 는 전체 데이터에 대한 E(w)을 최소화하는 가중치를 찾는 것이다. 따라서, E(w) 표면에 대해 Local minina가 많이 존재한다. 하지만, Stochastic Gradient Descent는 데이터 각각에 대한 E(w)을 최소하하는 가중치를 찾는 것으로 Local minima 의 위치가 다르게 존재하여, 결국 공통적으로 존재하는 Global minima 에 도달하는 가중치를 찾을 확률이 높다.

(3) 동일한 조건에서 초기랜덤생성한 가중치를 통해 다수의 네트워크를 학습하는 방법
- 동일학 학습데이터와 조건으로 네트워크를 다수 학습하고, 검증용(Validation) 데이터를 통해 가장 좋은 성능을 가진 네트워크를 선택한다.
6. Generalization for neural network
뉴럴네트워크가 Underfitting 이나 Overfitting 없이 학습하는 것은 새로운 데이터에 대해 원하는 결과를 얻기 위해 굉장이 중요하다. 이를 Generalization 이라고 표현하는데, 크게 두 가지 방법이 사용된다.
(1) Regularization
- 정규화라고 표현하며, 네트워크 가중치가 너무 낮은 값이어서 ill-conditioned 문제를 발생시키는 것을 w의 크기를 더해줘서 방지한다.

(2) Early Stopping
- 학습데이터를 Train, Validation 으로 나누어, 학습과정에서 Validation 데이터를 통해 주기적으로 네트워크의 성능을 검증하고, Validation 데이터에 대한 Error 가 상승하는 시점에서 학습을 종료하는 것이다.

'인공지능 > 머신러닝 이론' 카테고리의 다른 글
| 5-5. Introduction to Support Vector Machines(SVM) (0) | 2021.04.04 |
|---|---|
| 5-4. Radial Basis Function(RBF) Neural Network (0) | 2021.04.04 |
| 5-2. Multi-Layer Perceptron(MLP) Neural Network (0) | 2021.04.03 |
| 5-1. Introduction to Neural Networks (0) | 2021.04.03 |
| 4-5. Projection Pursuit (PP) (0) | 2021.04.02 |



